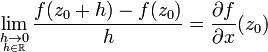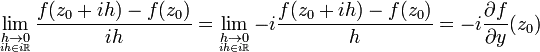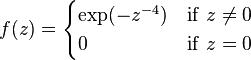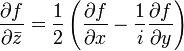Matematiğin bir dalı olan karmaşık analizde Augustin Louis Cauchy ve Bernhard Riemann'a atfen Cauchy-Riemann denklemleri olarak adlandıran denklemler, türevlenebilir bir fonksiyonun açık bir kümede holomorf fonksiyon olması için gerekli ve yeterli şartları sağlayan kısmi diferansiyel denklemlerdir. Bu denklemler sistemi ilk defa Jean le Rond d'Alembert'in 1752 yılındaki çalışmasında ortaya çıkmıştır. Daha sonra, 1777 yılındaki çalışmasıyla Leonhard Euler bu sistemi analitik fonksiyonlarla ilişkilendirmiştir. Cauchy ise bu sistemi 1814'teki çalışmasındaki fonksiyonlar teorisinde kullanmıştır. Riemann'ın fonksiyonlar teorisi üzerine olan doktora tezinin tarihi ise 1851'dir.
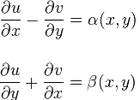
Bir gerçel değerli fonksiyon çifti u(x,y) ve v(x,y) için yazılan Cauchy-Riemann denklemleri aşağıdaki gibidir:
ve
Genelde u ve v çifti, karmaşık değerli bir f(x + iy) = u(x,y) + iv(x,y) fonksiyonunun gerçel ve sanal kısımları olarak alınır. u ve v, C 'nin açık bir kümesinde sürekli şekilde türevlenebilir bir fonksiyon olsun. O zaman, f=u+iv ancak ve ancak u ve v Cauchy-Riemann denklemlerini ((1a)'yı ve (1b)'yi) sağlarsa, holomorftur.
Yorumu ve formülasyonu
Açıkorur gönderimler
Cauchy-Riemann denklemleri çeşitli yollarla genelde tekrar formüle edilirler. Birincisi,
(2)
karmaşık formunda yazılabilirler.
Bu formda, denklemler yapısal olarak Jakoben matrisinin,
ve
olacak şekilde,
formunda olmasına karşılık gelir. Bu formdaki bir matris bir karmaşık sayının matris temsilidir. Geometrik olarak, böyle bir matris her zaman homotetisi olan bir rotasyonun bileşkesidir ve bilhassa açıları korur. Sonuç olarak, türevi sıfırdan farklı, Cauchy-Riemann denklemlerini sağlayan bir fonksiyon düzlemdeki eğriler arasındaki açıyı korur. Yani, Cauchy-Riemann denklemleri bir fonksiyonun açıkorur gönderim olması için olan koşullardır.
Karmaşık eşleniğin bağımsız olması
Cauchy-Riemann denklemleri bir fonksiyonun karmaşık türevli (veya holomorf) olması için gerekli ve yeterli bir koşuldur (Ahlofors 1953, §1.2 ). Daha ayrıntılı bir şekilde,
f(z) = u(z) + iv(z)
z ∈ C karmaşık sayısının fonksiyonu olsun. O zaman, f 'nin z0 noktasında karmaşık türevi eğer limit varsa
olarak tanımlanır.
Eğer bu limit varsa, limit reel eksen veya sanal eksen boyunca h → 0 alınarak hesaplanabilir ve her iki durumda da aynı sonucu vermelidir. Reel eksen boyunca yaklaşılırsa
elde edilir. Diğer taraftan sanal eksen boyunca yaklaşılırsa
elde edilir. İki eksen boyunca alınan türevlerin eşitliği
ifadesini verecektir. Farkedilirse bu, z0 noktasındaki (2) nolu Cauchy-Riemann denklemidir.
Tersine, f:C → C, R2 'de türevli olarak algılanırsa, o zaman f ancak ve ancak Cauchy-Riemann denklemleri sağlanırsa karmaşık türevlidir.
Diğer temsiller
Cauchy-Riemann denklemlerinin diğer temsilleri diğer koordinat sistemlerinde de ortaya çıkmaktadır. Sürekli şekilde türevlenebilir bir u ve v fonksiyon çifti için (1a) ve (1b) sağlanıyorsa, o zaman
'nin birim dik ve pozitif yönlü olduğu herhangi (n(x,y), s(x,y)) koordinatı için de
eşitlikleri sağlanır. Sonuç olarak, özellikle, z=reiθ olarak verilen kutupsal koordinatlar sisteminde, denklemler
halini alır.
f için bu iki denklem birleştirildiğinde
elde edilir.
Homojen olmayan denklemler
Homojen olmayan Cauchy-Riemann denklemleri, R2 'nin açık bir altkümesinde verilmiş α(x,y) ve β(x,y) için, bilinmeyen iki gerçel değişkenli bir u(x,y) ve v(x,y) fonksiyon çiftinin iki denkleminden oluşur:
Bu denklemler genellikle bir denklemde toplanırlar (f=u+iv ve φ=(α+iβ)/2)
Eğer φ, Ck ise, o zaman herhangi sınırlı bir D bölgesinin kapanışında φ sürekli olduğu sürece, homojen olmayan denklem D 'de açık olarak çözülebilir. Aslında Cauchy integral formülü kullanılarak her ζ ∈ D için
f = u+iv, f : R2 → R2 fonksiyonu olarak karmaşık değerli, türevlenebilir bir fonksiyon olsun. O zaman Goursat teoremi, f 'nin açık karmaşık bir Ω bölgesinde ancak ve ancak fonksiyon Cauchy-Riemann denklemlerini sağlarsa analitik olacağını ifade eder (Rudin 1966, Teorem 11.2). Özelde, f 'nin sürekli türevliliği varsayılmak zorunda değildir (Dieudonné 1969, §9.10, Al. 1).
Goursat teoremi 'nin varsayımları önemli bir ölçüde zayıflatılabilir. f=u+iv açık bir Ω kümesinde sürekliyse ve f 'nin Ω'da x ve y 'ye göre kısmi türevleri varsa, o halde f holomorftur (ve bu yüzden analitiktir). Bu sonuç Looman–Menchoff teoremi olarak bilinir.
f 'nin Ω üzerinde Cauchy-Riemann denklemlerini sağlaması varsayımı çok önemlidir. Bir noktada Cauchy-Riemann denklemlerini sağlayan ancak analitik olmayan bir fonksiyon inşa etmek mümkündür (mesela f(z) = z5/|z|4). Benzer bir şekilde, aşağıdaki örneğin de gösterdiği gibi, Cauchy-Riemann denklemlerinin yanında (süreklilik gibi) bazı ek varsayımlara da ihtiyaç vardır (örnek Looman 1923, sf. 107'dedir.):
Cauchy-Riemann denklemlerini sağlar ancak z=0 noktasında sürekli değildir.
Yine de, bir fonksiyon açık bir küme üzerinde Cauchy-Riemann denklemlerini zayıf bir anlamda sağlıyorsa, o zaman fonksiyon analitiktir. Daha kesin bir anlamda (Gray Morris 1978, Teorem 9),
f(z), Ω ⊂ C açık bölgesinde yerel olarak integrallenebiliyorsa ve zayıf bir şekilde Cauchy-Riemann denklemlerini sağlıyorsa, o zaman f, Ω içindeki analitik bir fonksiyonla hemen hemen her yerde aynıdır.
Çok değişkenler
Cauchy-Riemann denklemlerinin çok karmaşık değişkenlere uygun genelleştirmeleri de vardır. Kısmi diferansiyel denklemleri önemli bir artık belirtilmiş sistemlerini oluştururlar. Çoğu zaman formüle edildiği gibi
d-bar operatörü holomorf fonksiyonları imha eder. Bu doğrudan
