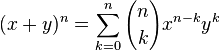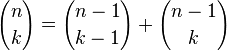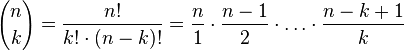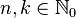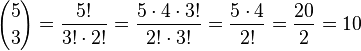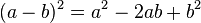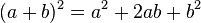Blaise Pascal
Fransız matematikçi ve felsefeci.
19 Haziran 1623 Clermont'da doğdu, 19 Ağustos 1662'de öldü.
Pascal, henüz küçük yaşta kendisini gösteren dehalardandır. Henüz 12 yaşındayken, hiç geometri bilgisine sahip olmadığı halde, daireler ve eşkenar üçgenler çizmeye başlamış, bir üçgenin iç açılarının toplamının iki dik açıya eşit olduğunu kendi kendine bulmuştur. Avukat olan ve matematikle çok ilgilenen babası, onun Yunanca ve Latince'yi iyi öğrenmeden matematiğe yönelmesini istemiyordu. Bu nedenle bütün matematik kitaplarını saklayarak Pascal'ın bu konu ile ilgilenmesini yasaklamıştır.

Pascal, çocukluğunda "Geometri neyi inceler?" sorusunu babasına sormuş ve "doğru biçimde şekiller çizmeyi ve şekillerin kısımları arasındaki ilişkileri inceler" cevabını almıştır. Pascal, bu cevaba dayanarak, gizli gizli geometri teoremleri kurmaya ve kanıtlamaya başlamıştır. Sonunda babası, onun yeteneğini anlamış ve ona Öklid'in (Euclid) Elementler'ini ve Apollonius'un Konikler'ini vermiştir. Dil derslerinden arta kalan zamanlarında babasının verdiği kitapları okuyan Pascal, 16 yaşında konikler üzerine bir eser yazmıştır. Bu eserin mükemmelliği karşısında Descartes, eserin Pascal gibi genç biri tarafından yazılmış olduğuna inanmakta güçlük çekmiştir.Pascal, 19 yaşında, aritmetik işlemlerini mekanik olarak yapan bir hesap makinesi icat etmiştir. Pascal yalnızca teorik bilimlerde değil, pratik ve deneysel bilimlerde de yetenekli ve özgün bir araştırmacıydı. 23 yaşında, Toricelli'nin atmosfer basıncı ile ilgili çalışmasını incelemiş ve bir dağa çıkartılan barometredeki cıva sütununun düştüğünü, yani yükseğe çıkıldıkça hava basıncının azaldığını göstermiştir. Diş ağrısından uyuyamadığı bir gece rulet oyunu ve sikloid üzerine düşünmüş ve sikloid eğrisinin özelliklerini keşfetmiştir.Pascal, Fermat ile yazışarak, olasılık teorisini kurmuş ve bir binom açılımında katsayıları vermiştir. Pascal üçgeni'nin keşfi de ona aittir. Pascal, çok genç yaşlarda çok önemli çalışmaları tamamlamış ve matematiğin gelişimine çok önemli katkılar yapmıştır. Pascal, 25 yaşına geldiğinde kendisini felsefe ve dine adamış, 39 yaşında da ölmüştür. Pascal üçgeni, binom açılımındaki katsayıları bulmaya yarar. Pascal'ın bu üçgeni, olasılıklar kuramında da ustalıkla kullanılır. Bu üçgen, biyolojideki uygulamalar, matematik, istatistik ve pek çok modern fizik konularında uygulama alanı bulunur.